2.6 THE POWER OF ONE, BUT BIGGER!

EXERCISE 2.6 THE POWER OF ONE, BUT BIGGER!

Repeat the previous exercise, but use an increasingly bigger input alphabet set. Try the test with both lowercase and uppercase letters. Then try it with lowercase letters, uppercase letters, and numbers. Finally, try all printable characters (string.printable).

• How many total symbols are in each input set?

• How much longer does each run take?

---

• How many total symbols are in each input set?

Input set	Python equivalent	Number of total symbols
lowercase and uppercase letters	string.ascii_letters	52
lowercase letters, uppercase letters, and numbers	string.ascii_letters + string.digits	62
all printable characters	string.printable	100

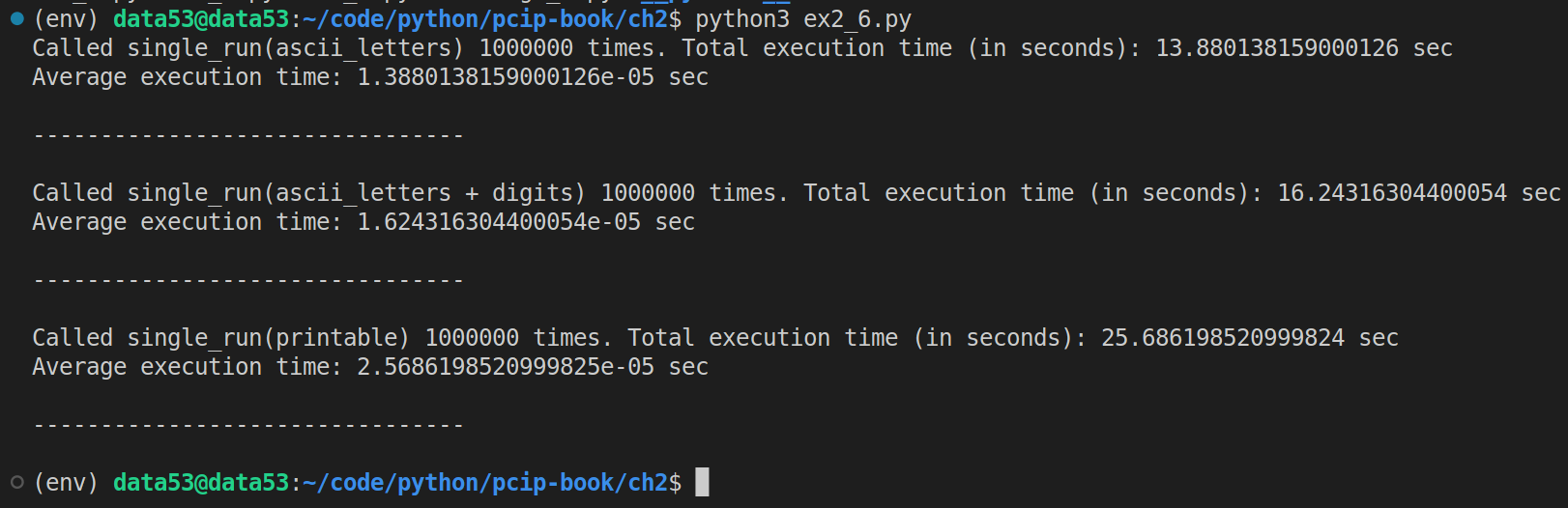
• How much longer does each run take?

I used the following code to answer this question:

# ex2_6.py 

import hashlib
import secrets
import timeit
from string import ascii_letters, digits, printable

possible_alphabets = {
    "ascii_letters": ascii_letters, 
    "ascii_letters + digits": ascii_letters + digits, 
    "printable": printable,
}

def single_run(alphabet_name: str): 
    alphabet = possible_alphabets[alphabet_name]
    
    def h(x: str) -> str:
        '''returns the md5 digest of the string x.'''
        return hashlib.md5(x.encode('utf-8')).hexdigest()

    preimage_seed = secrets.choice(alphabet)
    test_hash = h(preimage_seed)

    for single_letter in alphabet: 
        if h(single_letter) == test_hash: 
            # found a match
            break
    return 

if __name__ == '__main__':
    COUNTER = 1_000_000

    for alpha_name, alpha_value in possible_alphabets.items(): 
        total_execution_time = timeit.timeit(
            stmt=f"single_run('{alpha_name}')", 
            setup="from __main__ import single_run", 
            number=COUNTER, 
        )
        print(f"Called single_run({alpha_name}) {COUNTER} times. Total execution time (in seconds): {total_execution_time} sec")
        print(f"Average execution time: {total_execution_time/COUNTER} sec")
        print("\n--------------------------------\n")