3.8 XOR EXERCISE
EXERCISE 3.8: XOR EXERCISE
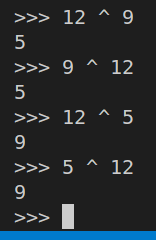
Because we will use XOR so much, it’s a good idea to get comfortable with XOR operations. In a Python interpreter, XOR a few numbers together. Python supports XOR directly using ^ as the operator. So, for example, 5^9 results in 12. What do you get when you try 12 ^ 9? What do you get when you try 12 ^ 5? Try this out with several different numbers.
Since we know that 5^9 = 12, we can deduce that
12 ^ 9 = (5 ^ 9) ^ 9 = 5 ^ (9 ^ 9) = 5 ^ 0 = 5
and
12 ^ 5 = (5 ^ 9) ^ 5 = (9 ^ 5) ^ 5 = 9 ^ (5 ^ 5) = 9 ^ 0 = 9
Fun facts abot XOR:
- XOR can be considered as the addition-modulo \(2\) operator in \(\text{Z} _2\) and hence satisfies the following properties:
- Associativity: (a ^ b) ^ c = a ^ (b ^ c)
- Identity Element: 0
- Commutativity: a ^ b = b ^ a
- The inverse of bit 0 is 0. The inverse of bit 1 is 1.
- a ^ a = 0
- a ^ 0 = a
Good articles about XOR: 1. https://accu.org/journals/overload/20/109/lewin_1915/ 2. https://florian.github.io/xor-trick/