4.12 RUN THE ATTACK!

EXERCISE 4.12: RUN THE ATTACK!

Take the preceding code and run some experiments with breaking RSA encryption with PKCS padding. You should use the cryptography module to create the encrypted message, convert the encrypted message to an integer, and then use your attack program (and fake oracle) to break the encryption. To begin with, test your program on RSA keys of size \(512\). This breaks faster and will enable you to validate your code sooner.

Step 1: Bob generates his private and public key pair (with key size 512 bits).

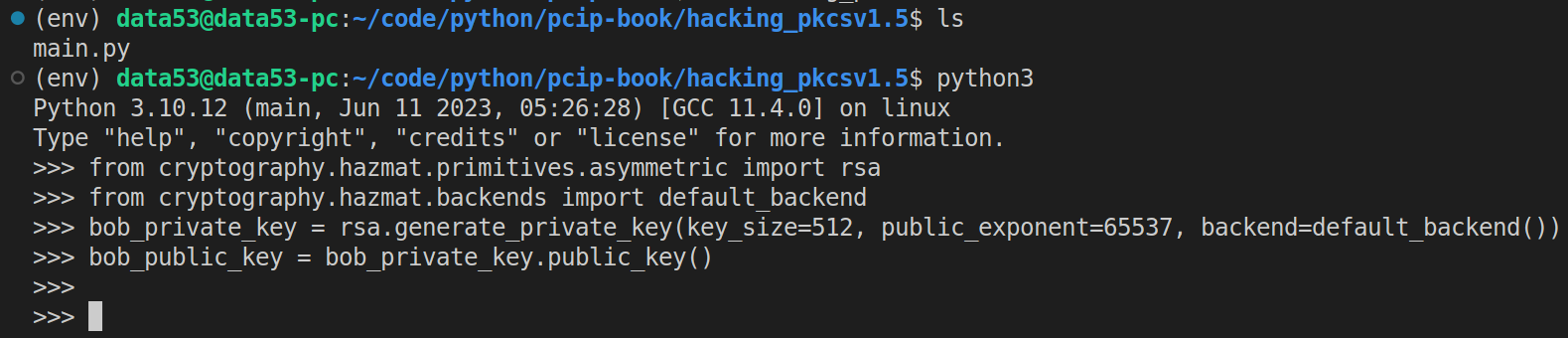
Step 2: Alice encrypts some data using bob’s public key.

Step 3: The oracle is assumed to be there, so create it…

Step 4: Eve intercepts Alice’s ciphertext and uses the oracle to launch the attack.

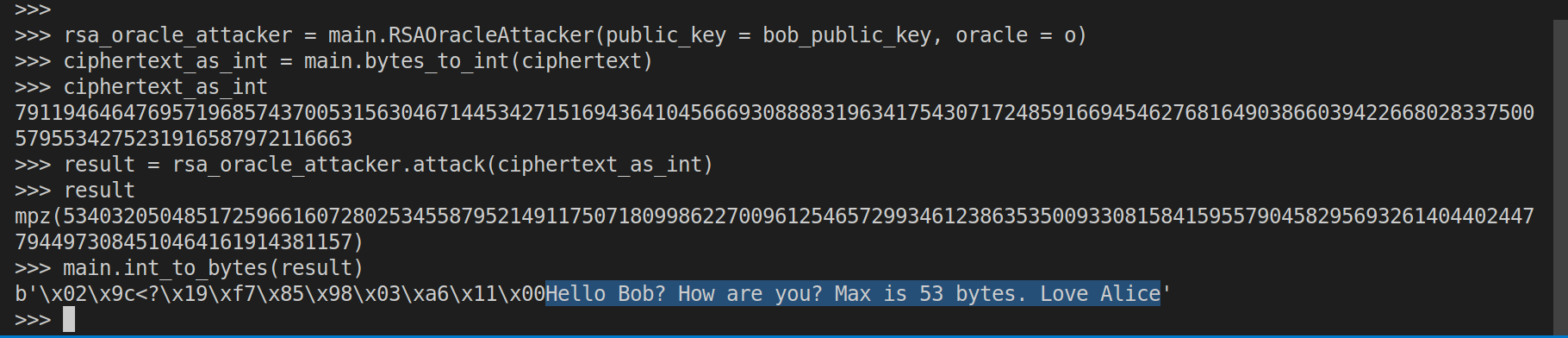
This was the key that was used in the above session:

This was the main.py file used in the above session:

from cryptography.hazmat.primitives.asymmetric import rsa, padding
from cryptography.hazmat.primitives.asymmetric.rsa import RSAPrivateKey, RSAPublicKey
from cryptography.hazmat.primitives import hashes,serialization 
from cryptography.hazmat.backends import default_backend 
import gmpy2 

from collections import namedtuple 

Interval = namedtuple('Interval', ['a', 'b']) 

def simple_rsa_encrypt(m, public_key): 
    numbers = public_key.public_numbers() 
    return gmpy2.powmod(m, numbers.e, numbers.n)

def simple_rsa_decrypt(c: int, private_key): 
    numbers = private_key.private_numbers() 
    return gmpy2.powmod(c, numbers.d, numbers.public_numbers.n)

def int_to_bytes(i, min_size=None):
    # i might be a gmpy2 big integer; convert back to a Python int. 
    i = int(i) 
    b = i.to_bytes((i.bit_length()+7)//8, byteorder='big')
    if min_size != None and len(b) < min_size: 
        b = b'\x00'*(min_size - len(b)) + b 
    return b 

def bytes_to_int(b): 
    return int.from_bytes(b, byteorder='big')

class Oracle: 
    pass 

class FakeOracle(Oracle): 
    def __init__(self, private_key): 
        self.private_key = private_key 
    
    def __call__(self,cipher_text:int)-> bool : 
        recovered_as_int = simple_rsa_decrypt(cipher_text, private_key=self.private_key)
        recovered = int_to_bytes(recovered_as_int, min_size=self.private_key.key_size//8) 
        return recovered[:2] == bytes([0, 2])
    

class RSAOracleAttacker: 
    def __init__(self, public_key: RSAPublicKey, oracle: Oracle): 
        self.public_key = public_key 
        self.oracle = oracle 
    
    def _step1_blinding(self, c): 
        self.c0 = c 
        
        self.B = 2 ** (self.public_key.key_size - 16)
        self.s = [1] 
        self.M = [ 
            [Interval(2 * self.B, 3 * self.B - 1)],
        ]

        self.i = 1 
        self.n = self.public_key.public_numbers().n 
    
    def _find_s(self, start_s, s_max = None): 
        si = start_s 
        ci = simple_rsa_encrypt(si, self.public_key) 

        while not self.oracle((self.c0 * ci) % self.n):
            si += 1 

            if s_max and (si > s_max): 
                return None 
            
            ci = simple_rsa_encrypt(si, self.public_key) 

        return si 
    
    def _step2a_start_the_searching(self): 
        si = self._find_s(start_s=gmpy2.c_div(self.n, 3 * self.B))
        return si 
    
    def _step2b_searching_with_more_than_one_interval(self): 
        si = self._find_s(start_s=self.s[-1] + 1) 
        return si 
    
    def _step2c_searching_with_one_interval_left(self): 
        a, b = self.M[-1][0]
        ri = gmpy2.c_div(2*(b*self.s[-1] - 2 * self.B), self.n) 
        si = None 

        while si == None: 
            si = gmpy2.c_div((2*self.B + ri * self.n), b) 
            s_max = gmpy2.c_div((3 * self.B + ri * self.n), a) 
            si = self._find_s(start_s = si, s_max = s_max) 
            ri += 1 
        
        return si 
    
    def _step3_narrowing_set_of_solutions(self, si): 
        new_intervals = set() 
        for a, b in self.M[-1]: 
            r_min = gmpy2.c_div((a*si - 3 * self.B + 1), self.n) 
            r_max = gmpy2.f_div((b*si - 2 * self.B), self.n) 

            for r in range(r_min, r_max + 1): 
                a_candidate = gmpy2.c_div((2 * self.B + r * self.n), si) 
                b_candidate = gmpy2.f_div((3 * self.B-1 + r * self.n), si) 

                new_interval = Interval(max(a, a_candidate), min(b, b_candidate)) 

                new_intervals.add(new_interval) 
        
        new_intervals = list(new_intervals) 
        self.M.append(new_intervals) 
        self.s.append(si) 

        if len(new_intervals) == 1 and new_intervals[0].a == new_intervals[0].b: 
            return True 
    
        return False 

    def _step4_computing_the_solution(self): 
        interval = self.M[-1][0] 
        return interval.a 
    
    def attack(self, c): 
        self._step1_blinding(c) 

        # do this until there is one interval left 
        finished = False 
        while not finished: 
            if self.i == 1: 
                si = self._step2a_start_the_searching()
            elif len(self.M[-1]) > 1: 
                si = self._step2b_searching_with_more_than_one_interval() 
            elif len(self.M[-1]) == 1: 
                interval = self.M[-1][0]
                si = self._step2c_searching_with_one_interval_left() 
            
            finished = self._step3_narrowing_set_of_solutions(si) 
            self.i += 1 
        
        m = self._step4_computing_the_solution() 
        return m