4.13 TAKING THE TIME
EXERCISE 4.13: TAKING THE TIME
How long does the attack take? Instrument your code with timing checks and a count of how many times the oracle function is called. Run the attack on a suite of inputs and determine the average amount of time to break keys of size $512, 1024, $ and \(2048\).
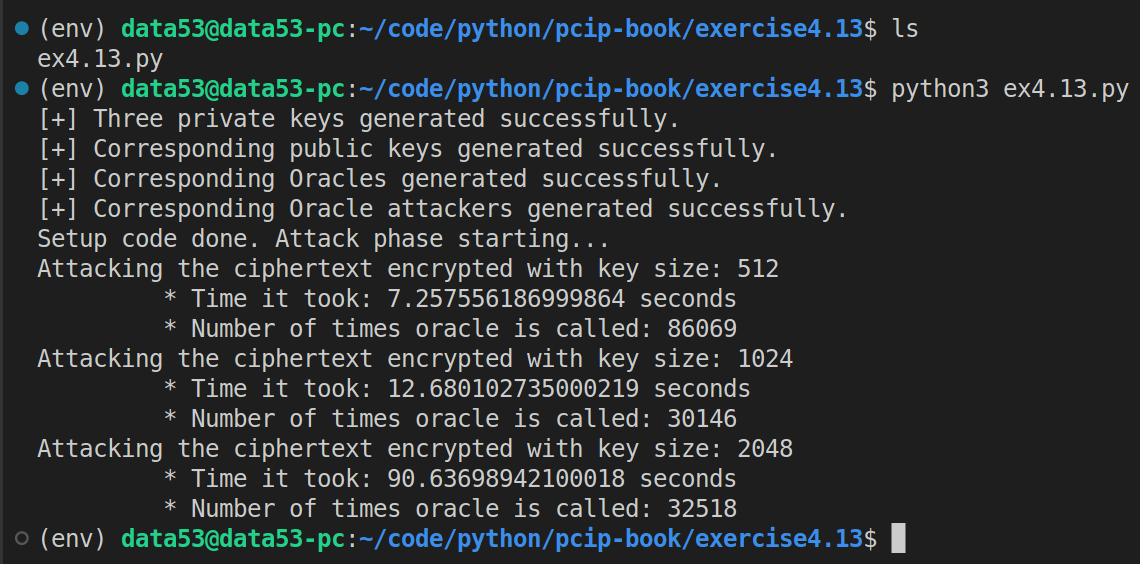
The code:
# ex4.13.py
from cryptography.hazmat.primitives.asymmetric import rsa, padding
from cryptography.hazmat.primitives.asymmetric.rsa import RSAPrivateKey, RSAPublicKey
from cryptography.hazmat.primitives import hashes,serialization
from cryptography.hazmat.backends import default_backend
import gmpy2
from collections import namedtuple
import timeit
Interval = namedtuple('Interval', ['a', 'b'])
def simple_rsa_encrypt(m, public_key):
numbers = public_key.public_numbers()
return gmpy2.powmod(m, numbers.e, numbers.n)
def simple_rsa_decrypt(c: int, private_key):
numbers = private_key.private_numbers()
return gmpy2.powmod(c, numbers.d, numbers.public_numbers.n)
def int_to_bytes(i, min_size=None):
# i might be a gmpy2 big integer; convert back to a Python int.
i = int(i)
b = i.to_bytes((i.bit_length()+7)//8, byteorder='big')
if min_size != None and len(b) < min_size:
b = b'\x00'*(min_size - len(b)) + b
return b
def bytes_to_int(b):
return int.from_bytes(b, byteorder='big')
class Oracle:
pass
class FakeOracle(Oracle):
def __init__(self, private_key):
self.private_key = private_key
self.counter = 0
def __call__(self,cipher_text:int)-> bool :
self.counter += 1
recovered_as_int = simple_rsa_decrypt(cipher_text, private_key=self.private_key)
recovered = int_to_bytes(recovered_as_int, min_size=self.private_key.key_size//8)
return recovered[:2] == bytes([0, 2])
class RSAOracleAttacker:
def __init__(self, public_key: RSAPublicKey, oracle: Oracle):
self.public_key = public_key
self.oracle = oracle
def _step1_blinding(self, c):
self.c0 = c
self.B = 2 ** (self.public_key.key_size - 16)
self.s = [1]
self.M = [
[Interval(2 * self.B, 3 * self.B - 1)],
]
self.i = 1
self.n = self.public_key.public_numbers().n
def _find_s(self, start_s, s_max = None):
si = start_s
ci = simple_rsa_encrypt(si, self.public_key)
while not self.oracle((self.c0 * ci) % self.n):
si += 1
if s_max and (si > s_max):
return None
ci = simple_rsa_encrypt(si, self.public_key)
return si
def _step2a_start_the_searching(self):
si = self._find_s(start_s=gmpy2.c_div(self.n, 3 * self.B))
return si
def _step2b_searching_with_more_than_one_interval(self):
si = self._find_s(start_s=self.s[-1] + 1)
return si
def _step2c_searching_with_one_interval_left(self):
a, b = self.M[-1][0]
ri = gmpy2.c_div(2*(b*self.s[-1] - 2 * self.B), self.n)
si = None
while si == None:
si = gmpy2.c_div((2*self.B + ri * self.n), b)
s_max = gmpy2.c_div((3 * self.B + ri * self.n), a)
si = self._find_s(start_s = si, s_max = s_max)
ri += 1
return si
def _step3_narrowing_set_of_solutions(self, si):
new_intervals = set()
for a, b in self.M[-1]:
r_min = gmpy2.c_div((a*si - 3 * self.B + 1), self.n)
r_max = gmpy2.f_div((b*si - 2 * self.B), self.n)
for r in range(r_min, r_max + 1):
a_candidate = gmpy2.c_div((2 * self.B + r * self.n), si)
b_candidate = gmpy2.f_div((3 * self.B-1 + r * self.n), si)
new_interval = Interval(max(a, a_candidate), min(b, b_candidate))
new_intervals.add(new_interval)
new_intervals = list(new_intervals)
self.M.append(new_intervals)
self.s.append(si)
if len(new_intervals) == 1 and new_intervals[0].a == new_intervals[0].b:
return True
return False
def _step4_computing_the_solution(self):
interval = self.M[-1][0]
return interval.a
def attack(self, c):
self._step1_blinding(c)
# do this until there is one interval left
finished = False
while not finished:
if self.i == 1:
si = self._step2a_start_the_searching()
elif len(self.M[-1]) > 1:
si = self._step2b_searching_with_more_than_one_interval()
elif len(self.M[-1]) == 1:
interval = self.M[-1][0]
si = self._step2c_searching_with_one_interval_left()
finished = self._step3_narrowing_set_of_solutions(si)
self.i += 1
m = self._step4_computing_the_solution()
return m
if __name__ == '__main__':
key_sizes_to_try = [512, 1024, 2048]
private_keys: list[RSAPrivateKey] = [
rsa.generate_private_key(
public_exponent=65537,
key_size=key_size,
backend=default_backend(),
)
for key_size in key_sizes_to_try
]
print("[+] Three private keys generated successfully.")
public_keys: list[RSAPublicKey] = [
single_private_key.public_key()
for single_private_key in private_keys
]
print("[+] Corresponding public keys generated successfully.")
oracles: list[FakeOracle] = [
FakeOracle(private_key=single_private_key)
for single_private_key in private_keys
]
print("[+] Corresponding Oracles generated successfully.")
msg = b'Hello Bob? How are you? Max varies. Love Alice'
ciphertexts = [
public_key.encrypt(
plaintext = msg,
padding = padding.PKCS1v15(),
)
for public_key in public_keys
]
rsa_oracle_attackers: list[RSAOracleAttacker] = [
RSAOracleAttacker(public_key=public_key, oracle=oracle)
for public_key, oracle in zip(public_keys, oracles)
]
print("[+] Corresponding Oracle attackers generated successfully.")
print("Setup code done. Attack phase starting...")
for key_size, attacker, c in zip(key_sizes_to_try, rsa_oracle_attackers, ciphertexts):
print(f"Attacking the ciphertext encrypted with key size: {key_size}")
c_in_int: int = bytes_to_int(c)
time_it_took = timeit.timeit(lambda: attacker.attack(c_in_int), number=1)
print(f"\t * Time it took: {time_it_took} seconds")
print(f"\t * Number of times oracle is called: {attacker.oracle.counter}")Note that this code does not answer the question fully. The question asks to give the code a “suite of inputs” and to take the average. I will leave that up to you. 😉